ANOVA: Understanding the Basics of Analysis of Variance

As a statistical method used to analyze data, ANOVA (Analysis of Variance) is one of the most widely used statistical techniques for comparing the means of two or more groups. In this article, we will delve deeper into the basics of ANOVA, its types, assumptions, and practical applications.

What is ANOVA?

ANOVA is a statistical method that is used to compare means between two or more groups. It does this by breaking down the total variance present in the data into two components: variance due to differences between groups and variance due to differences within groups. In essence, ANOVA is a way of testing whether the means of two or more groups are significantly different from each other.

Types of ANOVA

There are several types of ANOVA, each with its own specific use case. The most commonly used types of ANOVA include:

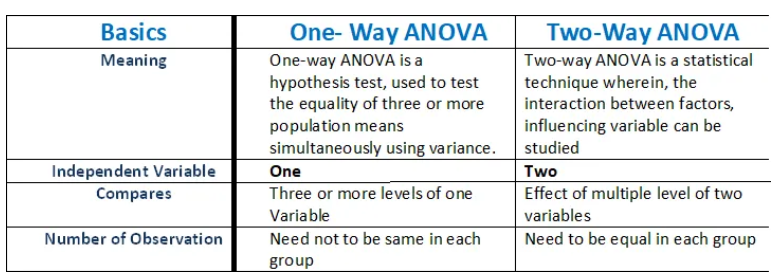
One-way ANOVA

One-way ANOVA is used to compare the means of two or more groups that are independent of each other. This type of ANOVA assumes that the samples are randomly selected and that the variances of the populations from which the samples are drawn are equal.

Two-way ANOVA

Two-way ANOVA is used to compare the means of two or more groups that are related to each other in some way. For example, it could be used to compare the means of two different drug treatments on patients of different ages. This type of ANOVA assumes that the samples are randomly selected and that the variances of the populations from which the samples are drawn are equal.

MANOVA

MANOVA (Multivariate Analysis of Variance) is used when there are two or more dependent variables that need to be analyzed simultaneously. It is used to test whether the mean vectors of the dependent variables are significantly different across the groups.

Assumptions of ANOVA

ANOVA is a powerful statistical tool, but it is also subject to several assumptions that must be met in order for it to be valid. These assumptions include:

Independence

The observations in each group must be independent of each other. This means that the outcome of one observation should not be influenced by the outcome of any other observation in the same group.

Normality

The distribution of each group should be approximately normal. This means that the mean and standard deviation of each group should be approximately the same.

Homoscedasticity

The variance of each group should be approximately the same. This means that the spread of each group should be approximately the same.

Sample size

The sample size of each group should be approximately the same. This means that each group should have a similar number of observations.

Practical Applications of ANOVA

ANOVA is used in many fields, including science, engineering, medicine, and social sciences. Some of the most common applications of ANOVA include:

Medical research

ANOVA is used to compare the effectiveness of different treatments or interventions in medical research.

Quality control

ANOVA is used in manufacturing to compare the quality of different products or production processes.

Marketing research

ANOVA is used in marketing to compare the effectiveness of different advertising campaigns or promotional strategies.

Education research

ANOVA is used in education research to compare the effectiveness of different teaching methods or curriculums.

Conclusion

In conclusion, ANOVA is a powerful statistical technique that is used to analyze the differences between multiple groups or conditions. It is widely used in many fields, including medicine, psychology, and engineering. By analyzing the sources of variation between and within groups, ANOVA can provide valuable insights into the factors that influence the outcome of an experiment.

However, it is important to keep in mind the assumptions of ANOVA and the limitations of the technique. Violations of the assumptions, such as non-normality or heteroscedasticity, can lead to invalid results. Additionally, ANOVA only provides information about whether there are significant differences between groups, but not which specific groups are different from each other. Finally, ANOVA is a parametric test that requires numerical data, so it may not be appropriate for all types of data.

Overall, ANOVA is a useful tool for analyzing differences between groups and can provide valuable insights into experimental data. By understanding the assumptions and limitations of ANOVA, researchers can use this technique to draw meaningful conclusions from their data.

If you want to learn more about statistical analysis, including central tendency measures, check out our comprehensive statistical course. Our course provides a hands-on learning experience that covers all the essential statistical concepts and tools, empowering you to analyze complex data with confidence. With practical examples and interactive exercises, you’ll gain the skills you need to succeed in your statistical analysis endeavors. Enroll now and take your statistical knowledge to the next level!

If you’re looking to jumpstart your career as a data analyst, consider enrolling in our comprehensive Data Analyst Bootcamp with Internship program. Our program provides you with the skills and experience necessary to succeed in today’s data-driven world. You’ll learn the fundamentals of statistical analysis, as well as how to use tools such as SQL, Python, Excel, and PowerBI to analyze and visualize data. But that’s not all – our program also includes a 3-month internship with us where you can showcase your Capstone Project.