The Central Limit Theorem (CLT) is one of the most important concepts in statistics, probability theory, and data analysis. It is the cornerstone of statistical inference and the foundation of many statistical methods. In this article, we will delve into the CLT, its underlying principles, and its applications in real-world scenarios.
Introduction to Central Limit Theorem
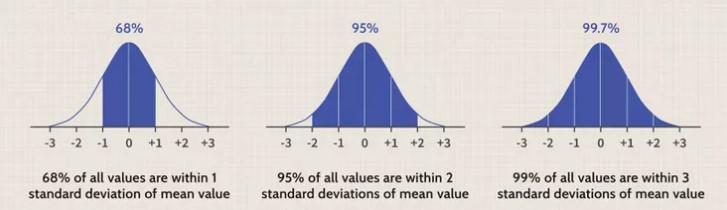
The Central Limit Theorem states that the sampling distribution of the mean of any independent, identically distributed random variables will be approximately normal, regardless of the original distribution of the variables. In simpler terms, the CLT asserts that the mean of a large sample of any variable will tend to follow a normal distribution, even if the variable itself is not normally distributed.
The Importance of Central Limit Theorem
The CLT is crucial in statistics because it allows us to make inferences about a population based on a sample. It provides a way to estimate the population parameters, such as the mean and standard deviation, with a certain degree of confidence, even if we only have a small sample size. It also helps us to analyze and interpret data, test hypotheses, and make predictions with more accuracy.
The Mathematics of Central Limit Theorem
The CLT is based on three important mathematical concepts: expectation, variance, and covariance. These concepts are essential to understand the underlying principles of the CLT.
Expectation
Expectation is the average value of a random variable, or the mean of a probability distribution. It represents the center of the distribution, around which the values tend to cluster. The expected value of a variable is calculated as the sum of the products of each value and its corresponding probability.
Variance
Variance is a measure of how spread out a distribution is. It represents the degree of variability or deviation from the mean. The variance of a variable is calculated as the sum of the squared deviations from the mean, divided by the number of observations.
Covariance
Covariance is a measure of the relationship between two variables. It indicates the degree to which the two variables are related or associated. The covariance between two variables is calculated as the sum of the products of the deviations of each variable from its mean, divided by the number of observations.
The Central Limit Theorem in Action
To better understand the CLT, let us consider an example. Suppose we want to estimate the average height of all adult males in the United States. It is impractical and impossible to measure the height of every male in the country, so we take a random sample of 100 men and measure their heights.
According to the CLT, the distribution of the sample mean should follow a normal distribution, regardless of the original distribution of the heights. This means that the sample mean should be approximately normally distributed, with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
By using the CLT, we can estimate the population mean and standard deviation with a certain degree of confidence, based on the sample mean and standard deviation. We can also use the normal distribution to make predictions about the heights of future samples.
The Limitations of Central Limit Theorem
Although the CLT is a powerful tool in statistics, it has some limitations and assumptions. The CLT assumes that the sample size is large enough and that the samples are independent and identically distributed. If the sample size is small or the samples are not independent or identically distributed, the CLT may not hold, and the sampling distribution may not be approximately normal.
Conclusion
The Central Limit Theorem is a fundamental concept in statistics and data analysis. It allows us to make inferences about a population based on a sample, estimate
If you want to learn more about statistical analysis, including central tendency measures, check out our comprehensive statistical course. Our course provides a hands-on learning experience that covers all the essential statistical concepts and tools, empowering you to analyze complex data with confidence. With practical examples and interactive exercises, you’ll gain the skills you need to succeed in your statistical analysis endeavors. Enroll now and take your statistical knowledge to the next level!
If you’re looking to jumpstart your career as a data analyst, consider enrolling in our comprehensive Data Analyst Bootcamp with Internship program. Our program provides you with the skills and experience necessary to succeed in today’s data-driven world. You’ll learn the fundamentals of statistical analysis, as well as how to use tools such as SQL, Python, Excel, and PowerBI to analyze and visualize data. But that’s not all – our program also includes a 3-month internship with us where you can showcase your Capstone Project.
